Design Optimization of an Airfoil Using Stanford University Software SU2

Stanford University Unstructured (SU2) is an open-source set of tools written in the C++ programming language. Designed to numerically solve problems involving Partial Differential Equations (PDEs), it is uniquely suited for PDE-constrained optimization problems. While Computational Fluid Dynamics (CFD) and aerodynamic shape optimization were influential in driving early development of the code, it has also proven useful in several other disciplines such as electrodynamics, linear elasticity, heat transfer, and chemically reacting flows. The Aerospace Design Laboratory (ADL), in Stanford’s Department of Aeronautics and Astronautics, is actively developing SU2, and external contributions from others are encouraged via their GitHub repository.
Computational analysis tools are an integral part of research, design, and product development in both academia and commercial environments–particularly within the aerospace industry. However, access to the source code for most established and reliable codes is either proprietary, prohibitively expensive, or otherwise unavailable. Similarly, procuring and maintaining the essential computing resources to run simulations is yet another barrier facing end-users. To help overcome this problem, the SU2 team provides an open-source, easy-to-use, and accurate flow solver, while Rescale offers its customers a scalable, on-demand, and enterprise-class computing platform, with SU2 among their available computational tools.
To demonstrate SU2’s aerodynamic shape optimization capabilities, we ran an inviscid, lift- constrained design optimization to minimize pressure drag for a half-symmetry ONERA M6 wing model (Figures 1a and 1b).
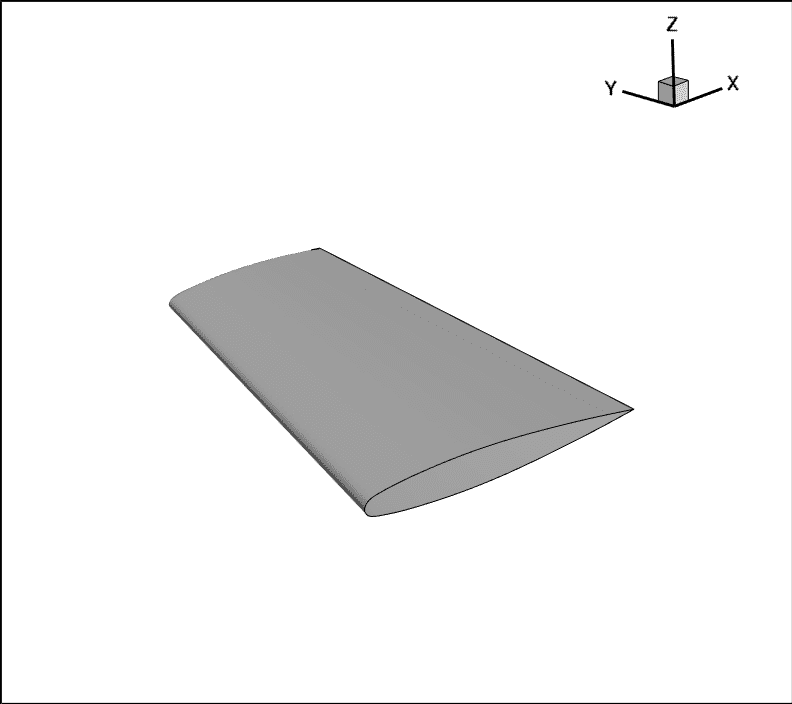
The ONERA M6 wing was designed in 1972 by the ONERA Aerodynamics Department as an experimental geometry for studying three-dimensional, high Reynolds number flows. This widely–known wing geometry serves as a reference model for validating new numerical methods and CFD codes due to the availability of empirical data and intriguing flow features. The analysis model surface mesh used in this design optimization is depicted.
Pressure: P0 = 2116 lb/ft2
Temperature: T0 = 32°F
Mach Number: M0 = 0.8395
Angle of Attack: α = 3.06°
Reference Area: A = 8.16 ft2
Lift Coefficient: CL ≥ 0.285
In drag minimization, it is appropriate to constrain the lift coefficient because the induced drag is a substantial component of the overall drag. Therefore, the total drag can reduced by simply reducing the lift. The solution proceeds by solving the direct flow problem, followed by solution of the continuous adjoint problem. Next the gradient for the objective function–pressure drag in this example–is calculated with respect to the movement of control points, or design variables. At each design iteration, the optimizer drives the shape changes, based on the computed gradients, in order to minimize the prescribed objective function and maintain lift. For our simulation, we ran sixteen design cycles and observed the results, highlighted in Figures 3a, 3b, and 4 below.
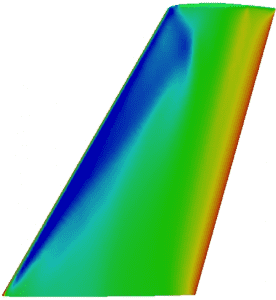

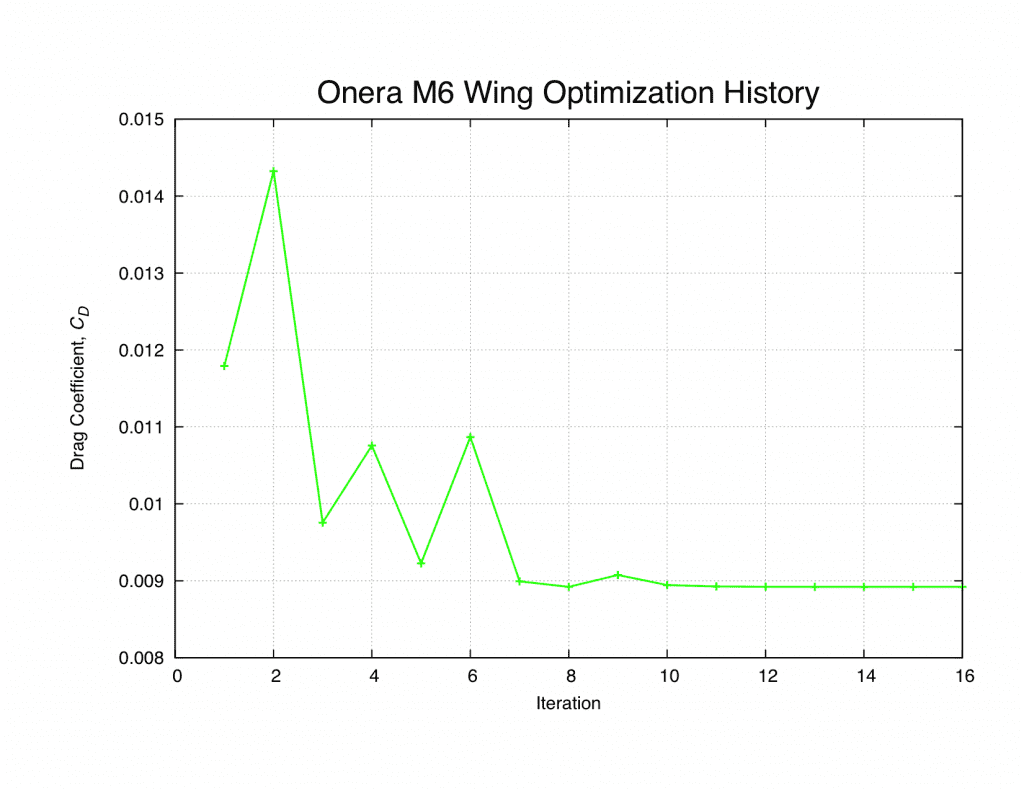
A comparison of the pressure contours on the upper wing surface is illustrated in Figures 3a & 3b. The initial direct flow solution is compared with results from the final iteration of the shape optimization. The sharp pressure rise, associated with a second shock wave further downstream of the initial shock, has been nearly eliminated. A plot of the drag coefficient, CD, with design cycle iteration is shown in Figure 4, highlighting how the pressure drag is reduced from roughly 0.0118 to 0.0089–a 24.6% reduction–over the course of the shape optimization.
For more information regarding SU2, please visit Stanford’s website at https://su2.stanford.edu. An active user community with direct feedback from SU2’s developers is available here. For information regarding setting up and running SU2 on Rescale, please contact us at support@rescale.com.