コストの比較: プリペイドとオンデマンド
Rescale はいくつかの製品を提供しています 価格オプション HPC シミュレーションを実行する場合: オンデマンド、低優先度、プリペイド。 この記事では、コストの観点からプリペイド プランを取得することが合理的かどうかを判断するためのコンピューティング使用量の分析を示します。
当社のプリペイド料金プランでは、予約の全時間分を前払いする代わりに、2 時間当たりの最低コストで Rescale コアを長期予約できます。 使用率が十分に高い場合、プリペイド コアはハードウェア コストを削減する優れた方法です。 以下、XNUMXつの質問に答えていきます。
- プリペイドで費用を節約するには、特定のコア タイプの使用率がどのくらい高くなければなりませんか?
- コアの使用スケジュールを考慮した場合、ハードウェアの総コストを最小限に抑えるには、プリペイド コアをいくつ購入すればよいでしょうか?
プリペイド利用によるコスト削減
最初の質問は、次の方程式を解くことで計算されます。
コスト削減 = 使用率 * 合計予約時間 * オンデマンド価格 – 合計予約時間 * プリペイド価格
プリペイド価格オプションでは 1 つの期間から選択できます。 ユーザーはコアを 3 年または 3 年分前払いできます。 したがって、人気のあるニッケル コア タイプ (0.04 年間の前払いコストは 0 ドル/コア/時間) の場合、コスト削減 = XNUMX となる損益分岐点は次のようになります。
使用率 = 0.04 時間あたり 0.15 ドル プリペイド / 27 時間あたり XNUMX ドル オンデマンド = ~ XNUMX%
ニッケルコアの平均使用率が上記を超えている場合 視聴者の38%が, プリペイドはオンデマンド料金と比較して費用を節約できます。 50 年間の平均使用率が XNUMX% であれば、節約になります。 コアごとに年間 482 ドル オンデマンドではなく、XNUMX 年間のプリペイド オプションを使用します。
特定の求人予測に対していくら前払いしますか?
上記の計算は単純ですが、目標使用率を念頭に置いていない場合があります。 代わりに、多くの場合、過去の使用状況に基づいて、実行を計画しているすべてのコンピューティング ジョブの予測を得ることができます。 ジョブのスケジュールを作成し、購入するプリペイド コアの最適な数を決定するにはどうすればよいでしょうか?
前と同様に、同様の計算を行います。
プリペイド節約額(x コアプリペイド) = すべてのオンデマンド コスト – (プリペイド コスト(x) + 残りのオンデマンド コスト(x))
すべてのオンデマンドのコスト プリペイド期間中のすべてのジョブの合計コア時間にオンデマンドのコア料金を掛けたものです。
前払い費用 は、x コアのプリペイド費用にすぎません。
残りのオンデマンドコスト 計算するのが難しいものです。 プリペイド コアの利用率を最大限に高めながら、必要な追加のオンデマンド コア時間を導き出す必要があります。
残りのコア時間を計算するには、単位時間あたりに実行されているコアの数を確認し、プリペイドではないコアのみを考慮する必要があります。 視覚的には、コアの使用時間間隔を下から上に詰め込み、時間内にジョブ全体で下位 x 個のコア (プリペイド コアを使用している) をスライスし、残りのコストを計算しています。
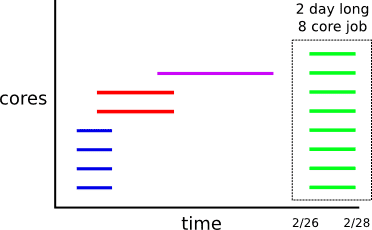
上の図は、コア時間間隔が必ずしも完全に重なったりバラバラになったりするわけではないことを考慮していません。 実際には、間隔をより小さなばらばらの間隔に分割し、これらの間隔部分を下から埋めていく必要があります。
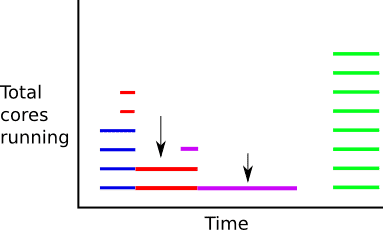
次に、タイム スライスごとにコアをカウントアップします。欠落しているスライスは暗黙的にコアがゼロになります。
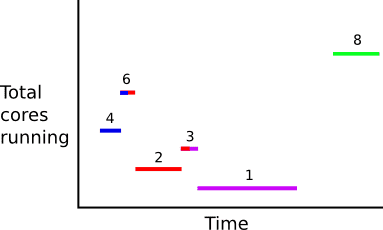
ここでは、ばらばらの間隔で予約期間を完全にカバーしました。 次に、プリペイド カウントを差し引くことができます。たとえば、プリペイド コアが 2 つある場合、これらの残りのコア間隔が得られます。
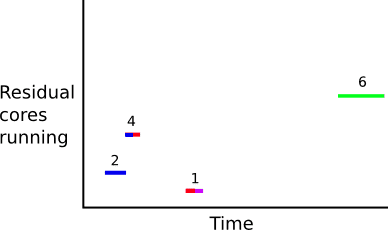
これらのインターバルから、インターバルの長さとコア数の積を合計して、残りのコア時間を取得します。
これと同じ分析をプログラムで行う方法を見てみましょう。 私たちの入力は次のとおりです。
- 計算ジョブのスケジュール。部分的に重複する (start_time、end_time、core_count) タプルのリストです。
- プリペイド予約期間の開始
- 前払い予約期間の終了
- プリペイドコアの数
def Calculate_residual_core_hours(core_use_intervals,reservation_start,reservation_end,prepaid_core_count): #start_timeでソートsorted_intervals =sorted(core_use_intervals, key=itemgetter(0))disjoint_intervals =chop_and_aggregate(reservation_start,reservation_end,sorted_intervals)residual_core_intervals = ((start_time, end_time, max(0) 、(count -paid_core_count))) for start_time、end_time、disjoint_intervals のカウント) return sum((end_time - start_time) * start_time、end_time のカウント、residual_core_intervals のカウント)
ここでの複雑さのほとんどは、chop_and_aggregate に隠されています。 これの実装を見てみましょう。 reservation_start から開始して、現在開いている間隔を追跡しながら、時間を進めていきます。 間隔が開くか閉じると、最後の 2 つの時間境界間の現在のコア数を使用して、新しい独立した間隔が作成されます。
def Chop_and_aggregate(reservation_start,reservation_end,sorted_intervals): current_time =reservation_start open_intervals = Counter() Closed_intervals = [] for start, end, count insorted_intervals: # 次の間隔が始まる前に終了する間隔を閉じる if open_intervals: next_end = min(open_intervals.keys ()) while start >= next_end: Closed_intervals.append((current_time, next_end, sum(open_intervals.values()))) del open_intervals[next_end] current_time = next_end if open_intervals: next_end = min(open_intervals.keys()) else : Break # 新しい間隔開始時刻でオープン間隔を分割 if open_intervals: Closed_intervals.append((current_time, start, sum(open_intervals.values()))) # 新しい間隔を追加 current_time = start open_intervals[end] += count # 終了終了の残りのオープン間隔 insorted(open_intervals.keys()): end = min(end,reservation_end) if open_intervals:closed_intervals.append((current_time, end, sum(open_intervals.values()))) del open_intervals[end]クローズドインターバルを返す
これらをすべてまとめると、残りのコア時間にオンデマンド価格を掛けて、コストを節約できます。 前払いコアをゼロにして Calculate_residual_core_hours を使用して、オールオンデマンドのコストを (非効率的に) 取得することもできます。
all_on_demand_hours =計算残余コア時間(ジョブ間隔、予約開始、予約終了、0) 残余オンデマンド時間 =計算残余コア時間(ジョブ間隔、予約開始、予約終了、プリペイドコア数) 節約 = (すべてのオンデマンド時間 * オンデマンド価格) - (プリペイドコア数 * プリペイド価格 + 残余オンデマンド_時間 * オンデマンド価格)
ここから、prepaid_core の数をバイナリ検索して、最適な節約額を見つけることができます。 最適化として、disjoint_intervals は、すべての異なる Prepaid コア計算に対して XNUMX 回計算するだけで済みます。
詳細
上記の説明は、実際のプリペイド オプションを簡略化したものです。
さまざまなコアの種類
通常実行するジョブ全体で複数のコア タイプ (マーブルとニッケルなど) を使用する場合があります。 その場合、ジョブをコア タイプごとに分離し、コア タイプのバッチごとに上記の分析を XNUMX 回実行します。 最終的には、各タイプの最適な数のプリペイド コアが得られます。 状況によっては、これにより容量が無駄になる可能性があることに注意してください。 特定のジョブに必要なコアよりも強力なコアで実行することになる場合でも、少数のコア タイプで実行するよりもコストが高くなる可能性があります。.
私たちは、以前の Rescale の使用状況に基づいて上記の分析を行って推奨事項を作成するプリペイド コア カリキュレーターを間もなくリリースする予定です。