高次 CFD シミュレーションに Rescale を活用する

経歴
計算流体力学（CFD） 過去数十年にわたって専門分野として大きな発展を遂げ、航空機、自動車、マイクロエレクトロニクス、その他いくつかの業界の製品設計における実証的テストを補完するために日常的に使用されています。 現在使用されている市販の流体フロー ソルバーの大部分は、有限差分法、有限体積法、または有限要素法を利用して、二次空間精度を達成しています。 これらの低次スキームは、多くの流れの問題に対して適切な精度を提供しながら、元の開発者側の多大な努力により、堅牢かつ手頃な価格になりました。
二次手法は産業界と学術界の両方で普及していますが、非常に低い数値散逸を必要とする、あまり適していない重要な流れの問題がいくつか存在します。 これらの流れの問題のほとんどには、渦支配の流れや航空音響の問題が含まれており、これらの流体の流れの問題の解決策は、構造化されていない高次の手法の助けがなければ解決が困難です。
二次精度では全体として許容できる解決策が得られない状況も発生します。 たとえば、ある変数 (揚力や圧力抗力など) の適切な解誤差が、別の変数 (せん断応力など) で許容できない解誤差を引き起こす可能性があります。 つまり、今日、高次の空間離散化を使用することが有利な流体の流れの問題がいくつか存在します。 これらの高次のスキームは、同等の計算コストで精度の向上を提供する可能性があります。
分析の説明
を使用して、複数の GPU コプロセッサ間で非構造化高次シミュレーションを実行するデモンストレーションを支援します。 のクラウドベースの HPC インフラストラクチャ、フローの計算 NACA 0012 翼形は、次の方法を使用して粘性亜音速流をシミュレートします。 PyFR¹。 2D 翼型上の層流のシミュレーションは決して目新しいものではありませんが、曲面メッシュ要素で離散化された計算領域を構成し、 フインさんの² 磁束再構成フレームワークと XNUMX 次元への拡張およびサブセルのショック捕捉スキーム³ CFD の現在の最先端技術について説明します。
支配方程式は、比熱の一定比が 1.4、プラントル数が 0.72 であるナビエ・ストークス方程式です。 粘性係数は次のように計算されます。 サザーランドの法則。 ここでは単一の流れ条件のみを考慮します。 M₀= 0.5と  α = 1^◦ 。 レイノルズ数、 Re = 5000、翼の翼弦長に基づいています。 NACA 0012 翼型は式 1 で定義されます。 (XNUMX) として:

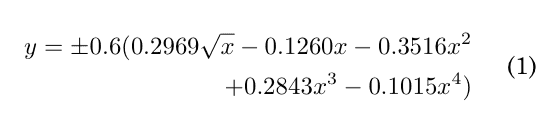
コラボレー ×∈ [0, 1]。 この式を使用して定義された翼形は、0.252% の有限の後縁を持ちます。 後縁の厚さがゼロになるようにこの定義を変更するさまざまな方法が文献に存在します。 ここで、x を変更するものは、⁴ 次のような係数が採用されます。

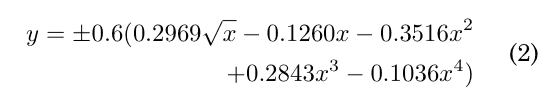
翼の形状は下の図(1)に示されています。

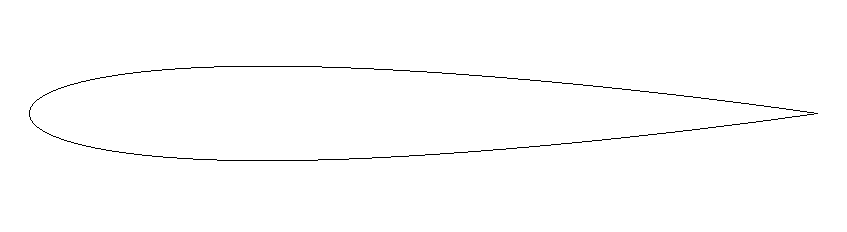
ファーフィールド境界条件は、亜音速の流入と流出に対してそれぞれ設定されます。 翼面は滑り止め断熱壁として設定されています。
8,960 個のクワッド要素で構成されるメッシュを使用して、流体ドメインを定義します。 XNUMX次曲線要素は次を使用して生成されます。 gmsh⁴、Christophe Geuzaine と Jean-François Remacle によって開発されたオープンソースの 1,000 次元有限要素メッシュ パッケージ。 ファーフィールド境界は、図に示すように、揚力係数と抗力係数に対するファーフィールド境界の影響に関連する問題を最小限に抑えるために、実際の翼形境界から 2 弦長以上離れた半径で翼の中央弦を中心とする円です。 .(XNUMX)

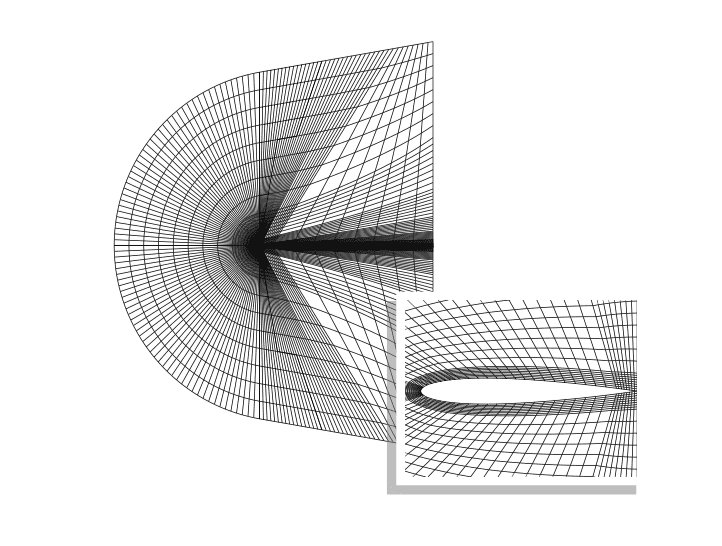
シミュレーションソリューション
PyFR は、さまざまな要素タイプを含む混合非構造グリッド上のさまざまな支配システムを解決するための効率的な高次移流拡散ベースのフレームワークを実装する、選ばれた数少ないオープン ソース プロジェクトの XNUMX つです。 PyFR は、Huynh の磁束再構成アプローチを推進するインペリアル カレッジ ロンドンの研究者チームによって積極的に開発が進められています。 PyFR は、従来の HPC クラスターに加えて、GPU クラスターやその他のストリーミング アーキテクチャ上で実行するために CUDA および OpenCL ライブラリを活用します。
Rescale は最近、GPU の「コア タイプ」を導入しました。これにより、エンドユーザーは独自の GPU クラスターを構成して、オンデマンドで複数のシミュレーションを実行できるようになります。 NVIDIA Tesla コプロセッサー カード。 これにより、ユーザーは大規模な計算離散化ドメインを小さなサブドメインに分解し、それぞれを専用の Tesla コプロセッサーで同時に実行することができます。

図 (2) に示す離散化された計算ドメインは 65 つの部分に分解され、シミュレーションは 4 つのノードと 20 つの NVIDIA Tesla コプロセッサーで構成される GPU クラスターを使用して Rescale で実行されました。 シミュレーションには単一の GPU で完全に実行できる 5.0 MB のメモリのみが必要なため、この方法でシミュレーションを分散することは単なる例示です。 05 次空間離散化 (p400,000) ソリューションは、XNUMXe-XNUMX 秒のタイム ステップ (つまり、合計 XNUMX ステップ) を使用して、陽的なルンゲ クッタ時間積分スキームを介して XNUMX 秒間時間的に進められました。

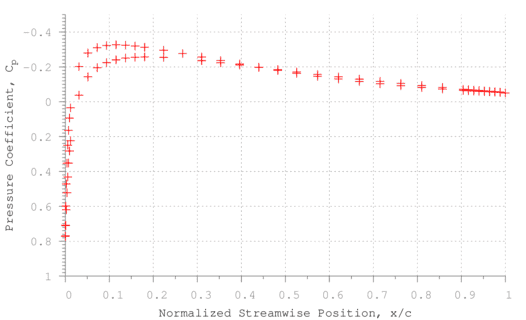
図 (3 と 4) は、マッハ等高線と圧力係数のシミュレーションから得られたプロットを示しています。 Cp 翼の表面周囲の分布。

揚力と抗力の係数は、シミュレーションの結果から次のように計算されました。

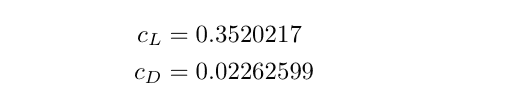
対応するエラーはそれぞれ 9.3876e-06 と 5.9600e-08 です。 ここで、誤差は 143,360 個のクワッド要素を使用して実行された参照ソリューションから計算されます。
まとめ
示されました⁵ PyFR で使用される Flux Reconstruction アルゴリズムは、他のよく知られた高次スキームを復元できることを示しています。 その結果、非構造化高次 CFD に対する統一的なアプローチ、またはフレームワークが提供されます。 これは、GPU やその他のストリーミング アーキテクチャでの実行にも特に適しています。 現在の CFD の進歩がより主流になるにつれて、この種のシミュレーションが実行されるコンピューティング ハードウェアの種類が変化する可能性があります。
Rescale は、ユーザーが独自のカスタム GPU クラスターをプロビジョニングして、マウスを数回クリックするだけで科学および工学に焦点を当てたさまざまなソフトウェア ツールを実行できるようにすることで、これらの進歩の最前線に位置しています。 Web ベースのインターフェイスを使用します。
ここ この記事の PDF コピーをダウンロードするには、 PyFR を試して実行してください。 独自のシミュレーション 今日はRescaleで。