数値流体力学 (CFD) ソリューションを理解する
数値流体力学がエンジニアや科学者による設計の分析と改良にどのように役立つかを理解する
エンジニアが新製品、たとえば次のレースシーズンの優勝レースカーの設計を任された場合、空気力学は設計の全体的なパフォーマンスにおいて重要な役割を果たします。 とはいえ、コンセプト段階では空力性能を簡単に定量化することはできません。
従来、エンジニアが設計を最適化する唯一の方法は、製品のプロトタイプで物理テストを実施することでした。 コンピューターの台頭と(ムーアの法則のおかげで)計算能力が増大し続けることにより、CFD の分野は現実世界の物理学を予測するために一般的に適用されるツールになりました。
数値流体力学 (CFD) は、重要な技術として浮上しています。 工学および科学研究。 CFD 解析は、流体の流れ、空気の流れ、熱伝達現象をシミュレートすることで、エンジニアや科学者が設計を分析および改良し、問題のトラブルシューティングを行い、複雑な流体の挙動を調査するのに役立ちます。
このブログではCFDの概要について説明します。 また、CFD の歴史について説明し、流体力学の基礎についても説明します。 さらに、CFD シミュレーションで使用される数値手法についても説明します。 最後に、CFD が適用されるさまざまな業界について説明します。
エンジニアリングと研究における CFD の価値
CFD は流体力学の分野の XNUMX つで、数値手法とコンピューター シミュレーションを使用して複雑な流体の流れの問題を解決します。 これにより、エンジニアや研究者は、流体の挙動を研究し、力と圧力を分析し、仮想環境でのパフォーマンスを予測することができます。
CFD ソフトウェアは、流体の流れ現象についての詳細な洞察を提供できるため、航空宇宙、自動車、エネルギー、生物医学などの幅広い業界で不可欠なツールとなっています。
数値流体力学の歴史
CFD のルーツは、エンジニアが流体の流れを記述するために数式を使用し始めた 1950 世紀初頭に遡ります。 しかし、CFD の大幅な進歩への道を開いたのは XNUMX 年代のデジタル コンピューターの出現でした。
計算能力の向上と高度な数値アルゴリズムの開発により、CFD は複雑な流体力学問題を正確かつ効率的に解決できる研究開発用の重要なツールに進化しました。
流体力学の原理
CFD の本質を理解するには、流体力学の基本概念を理解することが重要です。 このセクションでは、流体の特性、保存則、流体の流れの分類、流れの形態などの主要な原則について説明します。 粘度、密度、圧力、速度などの概念を探求し、CFD シミュレーションを推進する基礎的な原理を理解するための強固な基盤を提供します。
流体力学では、粘度は流体がどのように流れるかを決定する上で極めて重要な役割を果たします。 これは、せん断または流れに対する流体の抵抗を指し、温度や分子相互作用などの要因によって影響されます。 粘度を理解することは、蜂蜜のような高粘度の物質から水や空気のような低粘度の流体に至るまで、エンジニアが流体の挙動を分析するのに役立ちます。
密度
もう XNUMX つの重要な概念である密度は、流体の単位体積あたりの質量を表します。 浮力や圧力分布など、さまざまな条件下での流体の挙動に影響を与えます。 密度の変化を研究することで、エンジニアは流体の流れパターンについて洞察を得ることができ、層化や混合の存在を判断し、さまざまな環境における流体の挙動を予測できます。
圧力
圧力は流体力学の基本概念であり、単位面積あたりの流体によって及ぼされる力を表します。 圧力の変化は流体の動きをもたらし、流体の挙動を理解する上で重要な要素となります。 エンジニアは圧力分布を分析して構造に作用する力を評価し、効率的な流体輸送システムを設計し、さまざまな用途でのパフォーマンスを最適化します。
速度
速度は流体の流れの速度を指し、流体力学を理解する上で重要な役割を果たします。 これは、エンジニアが流れのパターンを決定し、流体の流れが構造に及ぼす影響を評価し、乱流や境界層の形成などの要因を分析するのに役立ちます。 これらの方法は、エンジニアや研究者が正確な CFD シミュレーションを行うのに役立ちます。 これらは流体の流れに関する洞察を提供し、設計を最適化し、工学および科学用途における意思決定に情報を提供します。
数値流体力学で使用される数値手法
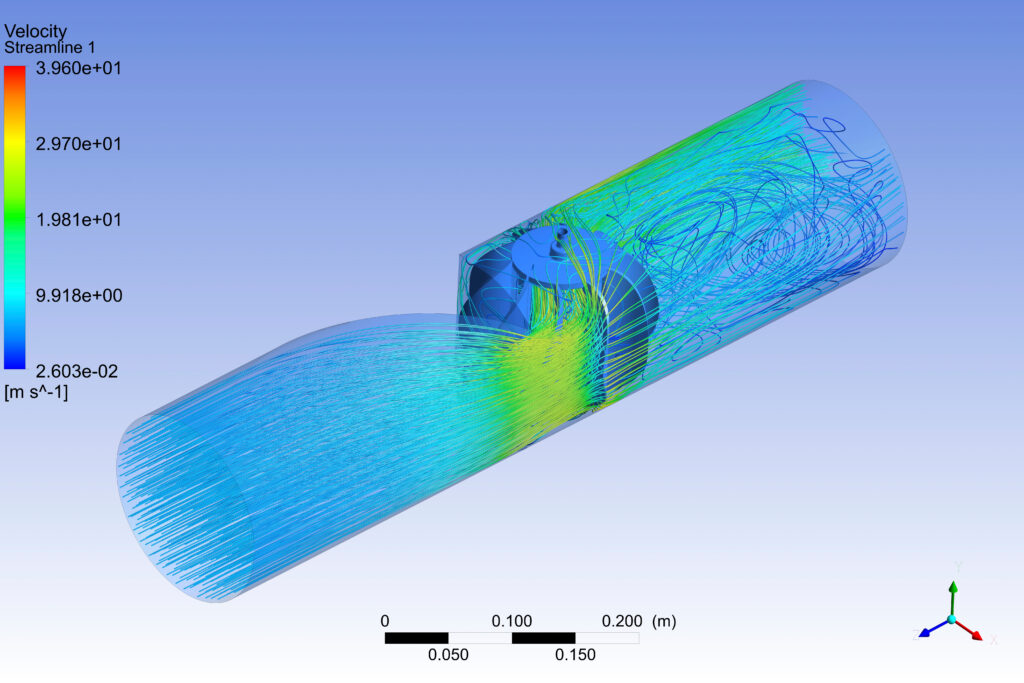
数値手法は CFD シミュレーションのバックボーンとして機能し、エンジニアや科学者が流体の流れの支配方程式を解くのに役立ちます。 このセクションでは、ナビエ・ストークス方程式に主に焦点を当てて、これらの方程式を離散化するために使用されるさまざまな数値手法を検討します。 連続方程式を離散形式に分解することにより、数値的手法は、計算を通じて複雑な流体の流れの問題を解決する道を開きます。
CFD で一般的に使用される XNUMX つの数値手法は、有限差分法、有限体積法、および有限要素法です。 各方法には、独自の利点、欠点、および適切な用途があります。
有限差分法は、離散差分方程式を使用して導関数を近似するため、単純かつ直感的になります。 一方、有限体積法は、制御体積内の質量、運動量、エネルギーの保存に重点を置き、正確で堅牢なソリューションを提供します。 最後に、有限要素法では、変分原理と要素の離散化を利用して、複雑な形状や境界条件を柔軟に処理できます。
数値手法に加えて、グリッド生成や境界条件などの CFD シミュレーションも現代のエンジニアリングの主要な側面です。 グリッドの生成には、計算領域を個別のセルまたは要素に分割することが含まれます。これらは、形状を正確に表現し、流体の流れの特徴を捉える上で重要な役割を果たします。
境界条件はドメイン境界における流体の挙動を定義し、現実的で信頼性の高い結果を得るために不可欠です。 さまざまな種類の境界条件がシミュレーションの精度と安定性に影響を与えます。
これらすべての方法は、正確で安定した CFD シミュレーションを実行するための基礎を形成し、エンジニアや研究者が流体の流れ現象に関する貴重な洞察を得て、設計を最適化し、さまざまな工学および科学アプリケーションで情報に基づいた意思決定を行うのに役立ちます。
業界を超えた CFD の応用
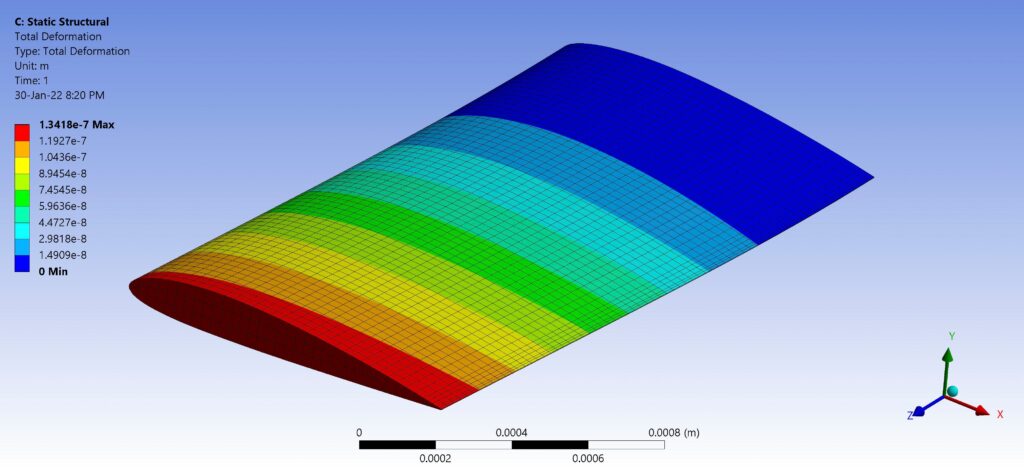
応力分布を示す数値応力シミュレーションとアニメーション。
スーパーコンピューティング能力によって駆動される数値流体力学は、工学および科学研究において非常に重要になっています。 CFD はさまざまな業界で広く応用されており、製品設計、最適化、問題解決に革命をもたらします。 CFDは次のような業界で活用されています。 航空宇宙, 自動車, エネルギー, 生物医学。 具体的な用途には、航空機や自動車の空力解析、発電所の熱管理、医療機器の血流シミュレーションなどがあります。
CFD シミュレーションの力を活用することで、産業界は設計を最適化し、流体の挙動を分析し、情報に基づいた意思決定を行うことができるため、イノベーションの限界を押し広げ、複雑な流体力学現象の理解を進めることができます。 CFD は、その変革的な影響により、工学および科学研究の未来を形作り続けています。
Rescale が数値流体力学 (CFD) シミュレーションにどのように役立つかについて詳しく知りたい場合は、弊社までお問い合わせください。 CFDの専門家.






