Understanding Computational Fluid Dynamics (CFD) Solutions
Understand how computational fluid dynamics helps engineers and scientists analyze and refine designs
When an engineer is tasked with designing a new product, e.g. a winning race car for the next race season, aerodynamics plays an important role in the overall performance of the design. That said, aerodynamic performance is not easily quantifiable during the concept phase.
Traditionally, the only way for an engineer to optimize his/her design is to conduct physical tests on product prototypes. With the rise of computers and ever-growing computational power (thanks to Moore’s law), the field of CFD has become a commonly applied tool for predicting real-world physics.
Computational fluid dynamics (CFD) has emerged as a critical technique in engineering and scientific research. By simulating fluid flow, air flow, and heat transfer phenomena, CFD analysis helps engineers and scientists analyze and refine designs, troubleshoot problems, and explore complex fluid behavior.
This blog will provide an overview of CFD. It will also discuss the history of CFD and explain the basics of fluid dynamics. Additionally, it will cover numerical methods used in CFD simulations. Finally, it will explore the various industries where CFD is applied.
The Value of CFD for Engineering and Research
CFD is a branch of fluid mechanics that employs numerical methods and computer simulations to solve complex fluid flow problems. It allows engineers and researchers to study fluid behavior, analyze forces and pressures, and predict performance in a virtual environment.
With its ability to provide detailed insights into fluid flow phenomena, CFD software has become an indispensable tool in a wide range of industries, including aerospace, automotive, energy, and biomedical.
The History of Computational Fluid Dynamics
The roots of CFD can be traced back to the early twentieth century when engineers started using mathematical equations to describe fluid flow. However, it was the advent of digital computers in the 1950s that paved the way for significant advancements in CFD.
With increasing computational power and the development of sophisticated numerical algorithms, CFD evolved into a critical tool for R&D capable of solving complex fluid dynamics problems accurately and efficiently.
The Principles of Fluid Dynamics
Understanding the fundamental concepts of fluid dynamics is crucial to grasp the essence of CFD. This section covers key principles such as fluid properties, conservation laws, fluid flow classification, and flow regimes. We will explore concepts like viscosity, density, pressure, and velocity, providing a solid foundation for comprehending the underlying principles driving CFD simulations.
Viscosity
In fluid dynamics, viscosity plays a pivotal role in determining how fluids flow. It refers to a fluid’s resistance to shear or flow and is influenced by factors such as temperature and molecular interactions. Understanding viscosity helps engineers analyze the behavior of fluids, ranging from highly viscous substances like honey to low-viscosity fluids like water or air.
Density
Density, another crucial concept, represents the mass per unit volume of a fluid. It affects fluid behavior under various conditions, such as buoyancy and pressure distribution. By studying density variations, engineers can gain insights into fluid flow patterns, determine the presence of stratification or mixing, and predict the behavior of fluids in different environments.
Pressure
Pressure is a fundamental concept in fluid dynamics, representing the force exerted by a fluid per unit area. Changes in pressure result in fluid motion and are key factors in understanding fluid behavior. Engineers analyze pressure distributions to evaluate forces acting on structures, design efficient fluid transport systems, and optimize performance in various applications.
Velocity
Velocity refers to the rate of fluid flow and plays a crucial role in understanding fluid dynamics. It helps engineers determine flow patterns, assess the impact of fluid flow on structures, and analyze factors like turbulence and boundary layer formation. These methods help engineers and researchers with accurate CFD simulations. They provide insights into fluid flow, optimize designs, and inform decisions in engineering and scientific applications.
Numerical Methods Used in Computational Fluid Dynamics
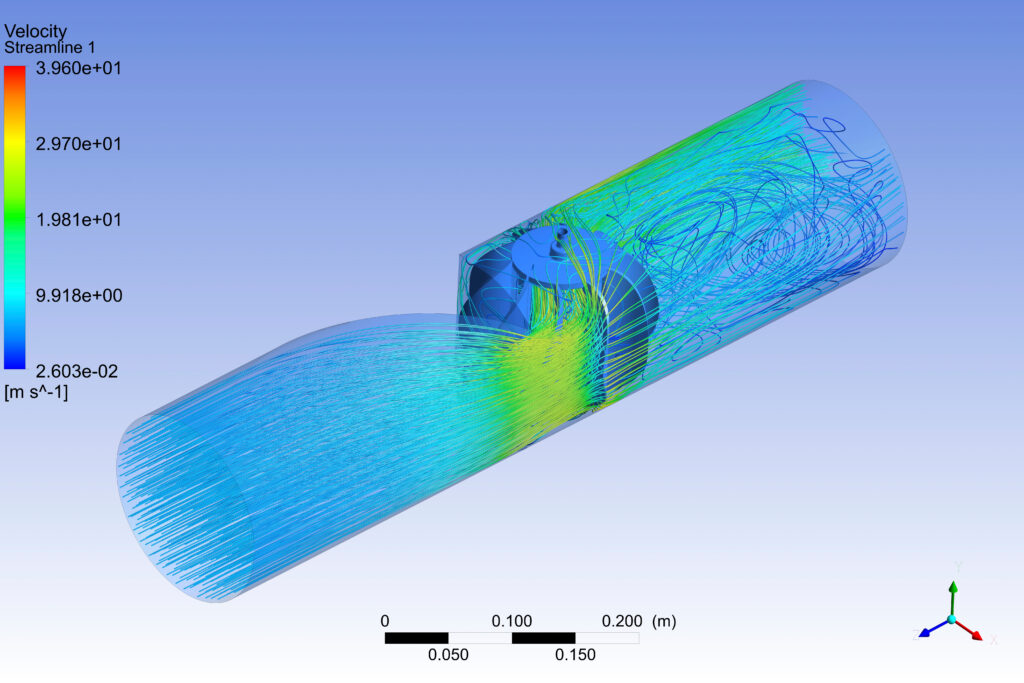
Numerical methods serve as the backbone of CFD simulations, helping engineers and scientists solve the governing equations of fluid flow. In this section, we explore the various numerical techniques used to discretize these equations, with a primary focus on the Navier-Stokes equations. By breaking down the continuous equations into discrete form, numerical methods pave the way for solving complex fluid flow problems through computation.
Three commonly employed numerical methods in CFD are finite difference, finite volume, and finite element methods. Each method possesses its own set of advantages, disadvantages, and suitable applications.
Finite difference methods approximate derivatives using discrete difference equations, making them straightforward and intuitive. Finite volume methods, on the other hand, focus on the conservation of mass, momentum, and energy within control volumes, offering accurate and robust solutions. Lastly, finite element methods utilize variational principles and element discretization to achieve flexibility in handling complex geometries and boundary conditions.
In addition to numerical methods, CFD simulations, such as grid generation and boundary conditions are a major aspect of modern engineering. Grid generation involves dividing the computational domain into discrete cells or elements, which play a vital role in accurately representing the geometry and capturing the fluid flow features.
Boundary conditions define the behavior of the fluid at the domain boundaries and are essential for obtaining realistic and reliable results. Different types of boundary conditions have implications on simulation accuracy and stability.
All these methods form the basis for conducting accurate and stable CFD simulations, helping engineers and researchers gain valuable insights into fluid flow phenomena, optimize designs, and make informed decisions in various engineering and scientific applications.
Applications of CFD Across Industries
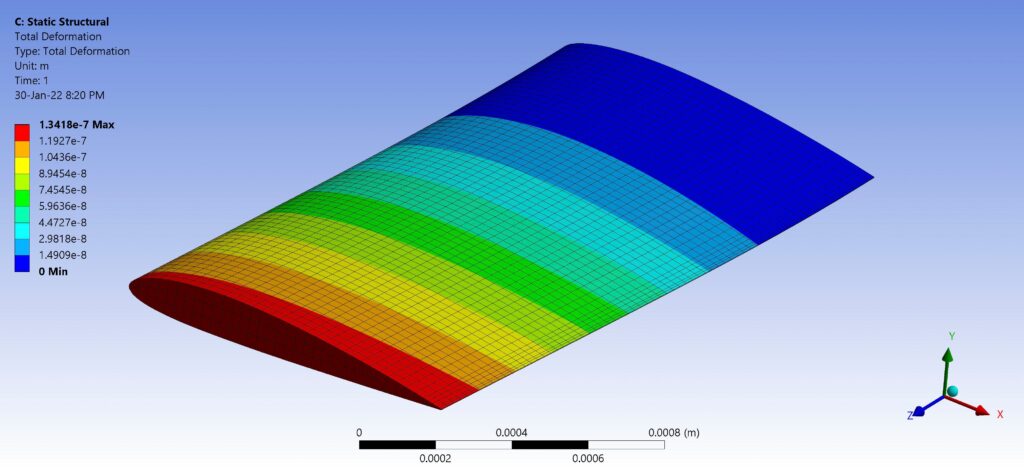
Numerical stress simulation and animation showing stress distribution.
Computational fluid dynamics driven by supercomputing power has become vitally important in engineering and scientific research. CFD finds widespread applications across diverse industries, revolutionizing product design, optimization, and problem-solving. CFD is utilized in industries such as aerospace, automotive, energy, and biomedical. Specific applications include aerodynamic analysis of aircraft and cars, thermal management in power plants, and simulation of blood flow in medical devices.
By harnessing the power of CFD simulations, industries can optimize designs, analyze fluid behavior, and make informed decisions, thereby pushing the boundaries of innovation and advancing our understanding of complex fluid dynamics phenomena. With its transformative impact, CFD continues to shape the future of engineering and scientific research.
To learn more about how Rescale can help with computational fluid dynamics (CFD) simulations please contact our CFD experts.






